8 (800) 775 4121
Назад
1 853
25 апреля 2024
ЕГЭ по профильной математике: новое задание на векторы
Статья 
Оглавление
В 2024 году в программе экзамена по математике профильного уровня всего одно изменение — в первой части добавили задачу № 2 на векторы. Новые задания можно условно разделить на две группы: сложение и координаты вектора.
Решения новой задачи на сложение векторов в ЕГЭ по математике мы уже подробно разобрали. И некоторые из вас уже справились с нашим тестом про сложение векторов. В этой статье просто и на примерах разберём вторую группу заданий и вместе решим задачи на координаты вектора в ЕГЭ по профильной математике.
Шпаргалка к задачам на координаты вектора
Для начала вспомним базу. Рассмотрим прямоугольную систему координат и выберем на ней два неколлинеарных вектора, длина которых равна единичному отрезку данной системы координат. Такие векторы называют координатными.
Важно также помнить, что любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициент разложения определяется единственным образом.
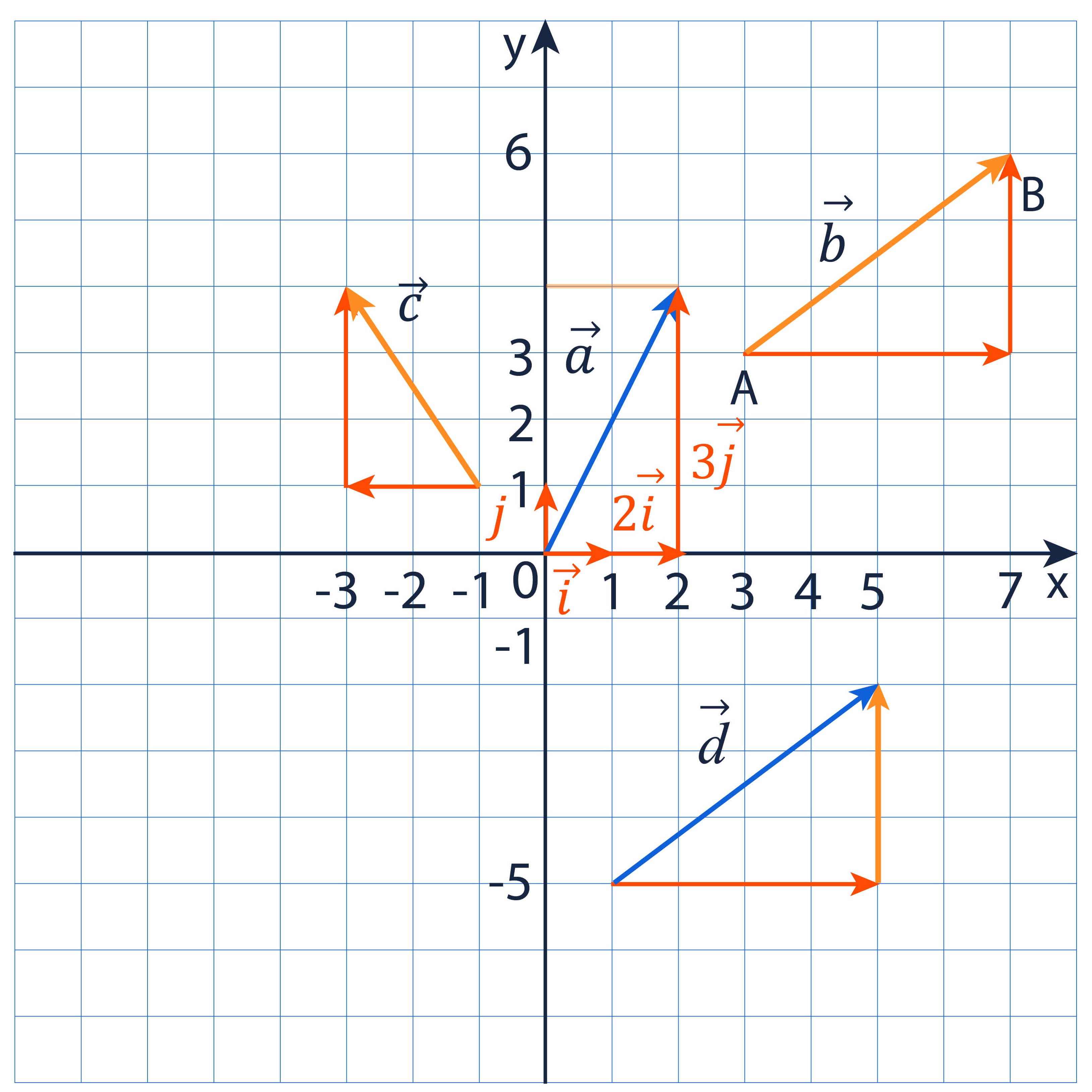
Особенности координат
Вектор, выходящий из начала координат, называется радиус-вектор. Координаты радиус-вектора равны координатам его конца.
Правила нахождения координат
Для того чтобы найти координаты вектора, не нужно каждый раз строить равный ему вектор из начала координат. Чтобы найти координаты вектора, необходимо из координат конца вычесть координаты начала.
Найти координаты суммы или разности векторов помогут простые правила:
каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов;
каждая координата разности двух или более векторов равна разности соответствующих координат этих векторов;
каждая координата произведения вектора на число равна произведению соответствующей координаты на это число.
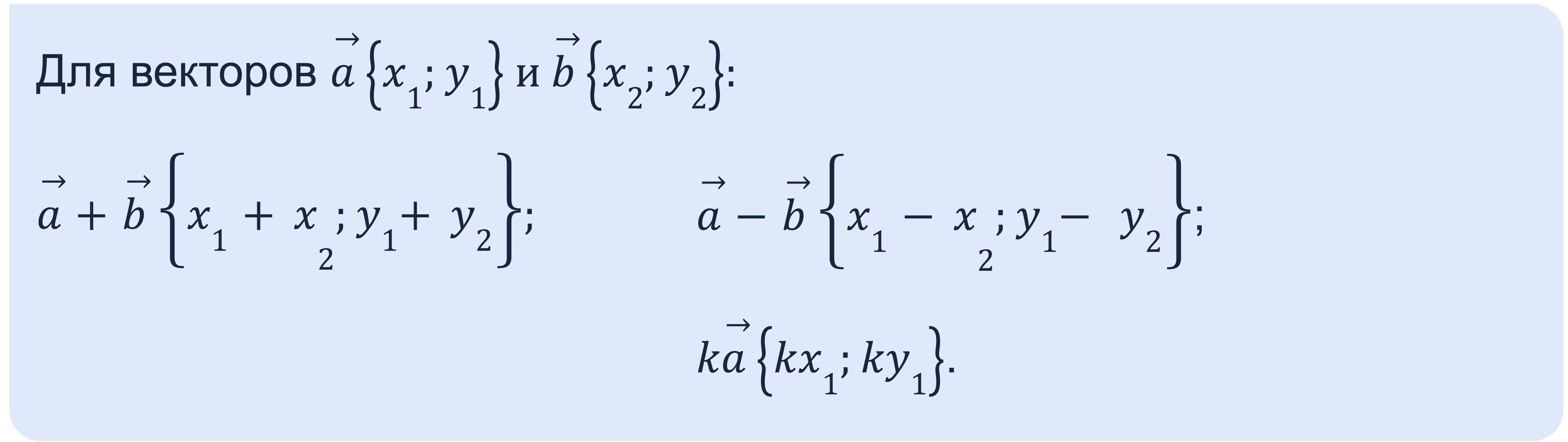
Положительный и отрицательный коэффициенты отношения
Отметим, что координаты коллинеарных векторов пропорциональны, причём если векторы сонаправлены, то коэффициент отношения положительный, а если противоположно направлены, то отрицательный.
Длина вектора через координаты
Через координаты вектора можно также найти его длину.
Скалярное произведение
Последним важным понятием, которое нам необходимо разобрать, является скалярное произведение — операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.
Скалярное произведение можно также записать в координатах, это будет сумма произведений соответствующих координат.
Теперь приравняем скалярное произведение, выраженное через длины векторов и косинус угла между ними, и скалярное произведение, выраженное через координаты векторов:
Таким образом, мы получили формулу, позволяющую найти угол между двумя векторами, когда известны их координаты.
Примеры решения новой задачи в ЕГЭ по математике
Теперь решим несколько задач, где применяется теория, которую мы только что рассмотрели.
Пример 1
Решение
Не забываем, что х — это абсцисса, а у — ордината.
В ответе просят дать только абсциссу, значит, выписываем 2.
Ответ: 2.
Пример 2
Решение
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Каждая координата произведения вектора на число равна произведению соответствующей координаты на это число.
В ответе просят записать сумму координат, то есть х + у = 4 + 33 = 37.
Ответ: 37.
Пример 3
Решение
Ответ: 5.
Пример 4
Решение
Ответ: 7,5.
Пример 5
Решение
Ответ: 60.
Вроде бы не так уж и страшно. Но это пока мы решаем вместе, а теперь самое приятное: практика. Предлагаем закрепить новые знания в нашем тренажёре на решение новых задач на координаты вектора.
Понимаем, самостоятельно разобраться в новой теме и подготовиться к ЕГЭ по профильной математике сложно. Но мучиться и необязательно. Можно сэкономить нервы, силы и время: быстрее разобраться вместе с профессиональными репетиторами. Например, с помощью экспертов нашей Домашней школы «ИнтернетУрок».
Начни подготовку заранее!
