Решение текстовых задач по математике в ОГЭ и ЕГЭ

Текстовые задачи по математике в ОГЭ и ЕГЭ
В 2024 году ищите текстовую задачу:
-
под номером 21 в ОГЭ по математике;
-
под номером 20 в ЕГЭ по математике базового уровня;
-
под номером 10 в ЕГЭ по математике профильного уровня.
Текстовые задачи можно разделить на пять групп: задачи на движение по прямой, задачи на движение по воде, задачи на работу, задачи на сплавы и смеси, задачи на прогрессии. В этой статье рассмотрим стандартные схемы решения, которые подходят для задач первых трёх групп.
Решение текстовых задач на движение по прямой
Большинство экзаменационных задач на движение по прямой можно решить при помощи алгоритма:
-
Составляем таблицу со столбцами: расстояние — S, скорость — V, время — t.
-
Обозначаем неизвестной х то, что требуется найти в задаче.
-
Заполняем два столбца таблицы в соответствии с введённой неизвестной и данными задачи.
-
Заполняем оставшийся «ключевой» столбец (чаще всего это столбец «Время») по формулам: S = V × t; V = S : t; t = S : V.
-
Составляем уравнение с данными ключевого столбца таблицы.
-
Решаем полученное уравнение и находим неизвестную.
-
Не забываем, что скорость, время и расстояние должны быть положительными.
В процессе выполнения задач будут получаться квадратные уравнения, для решения которых может потребоваться нахождение корня из большого числа. Если вы сдаёте ОГЭ или ЕГЭ базового уровня, то можете пропустить эту часть. В вашем справочном материале будет представлена таблица квадратов. Если же вы сдаёте профильный экзамен, советуем сосредоточиться и разобраться.
Допустим, при решении уравнения мы получили дискриминант, равный 5184.
Это число больше 100, но меньше 10 000. Значит, это квадрат двузначного числа. Ведь самое маленькое двузначное число (10) в квадрате даёт 100, а самое маленькое трёхзначное (100) в квадрате даёт 10 000.
Обратим внимание на последнюю цифру числа. Какое число от 1 до 9 в квадрате на конце даёт 4? Это либо 2, либо 8. Значит, наше двузначное число оканчивается либо на 2, либо на 8.
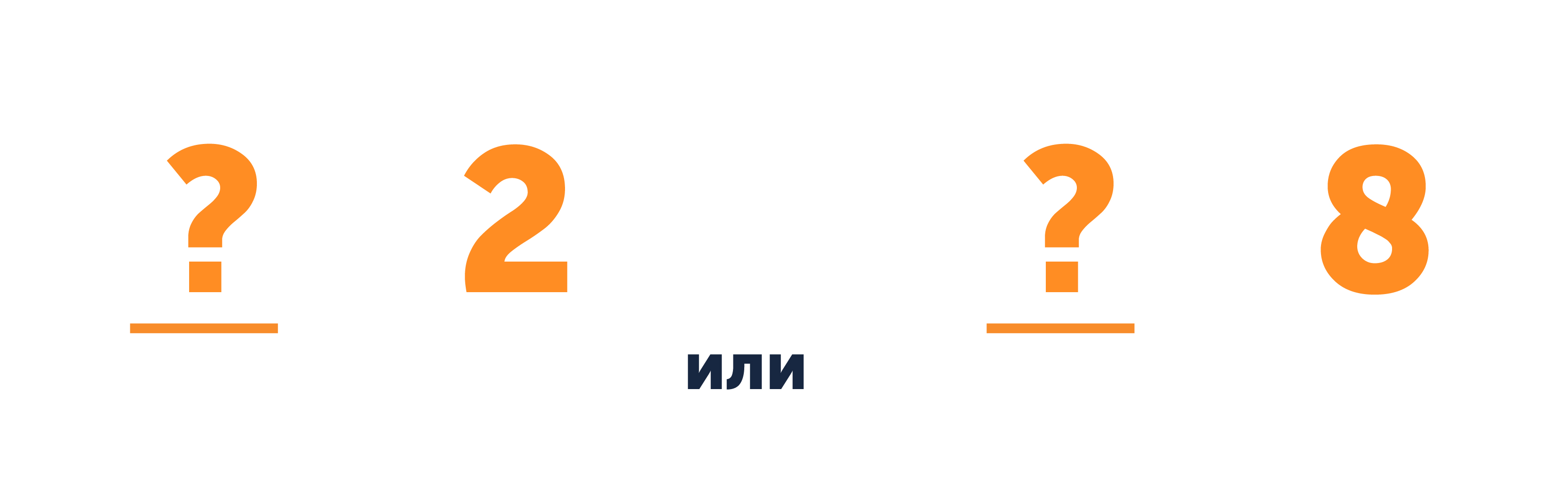
Теперь проверим круглые десятки, которые в квадрате дают числа, между которыми находится число 5184.
702 = 4900
802 = 6400
Значит, искомое число лежит в диапазоне от 70 до 80 и заканчивается либо на 2, либо на 8.
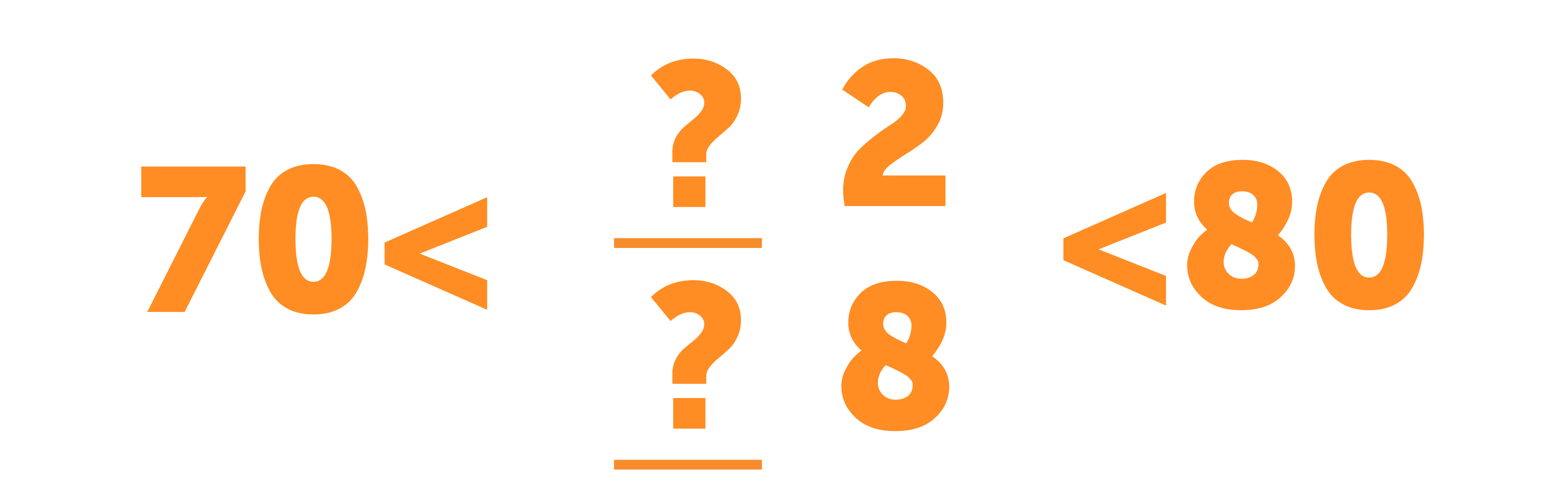
Получается, это либо 72, либо 78. Поскольку 5184 ближе к 4900, предполагаем, что это 72. Проверим результат умножением. Действительно, 72 × 72 = 5184.
Пример решения текстовой задачи из экзамена

Решение:
1. Составим таблицу и отметим героев задачи. Это автомобилист и велосипедист.
Заменим скорость велосипедиста, о которой спрашивают в задаче, на х. Автомобилист проезжает в час на 40 километров больше, значит, его скорость равна х + 40 км/ч.
Вносим информацию о расстоянии в соответствующий столбец таблицы (S). И автомобилист, и велосипедист проезжают расстояние от пункта А до пункта В, равное по условию 100 километрам.
Заполняем оставшийся, ключевой, столбец — время. Помним, что t = S : V. Получается, время движения автомобилиста равно 100 : (x + 40) часов, а велосипедиста — 100 : часов.

2. Найдём в тексте задачи дополнительное условие на время: велосипедист прибыл в пункт В на 8 часов позже автомобилиста. Получается, если из времени, которое потратил на дорогу велосипедист, мы вычтем время, которое потратил на дорогу автомобилист, мы получим 8 часов. Составим уравнение.
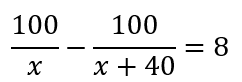
3. Разделим обе части уравнения на 4 для упрощения вычислений.
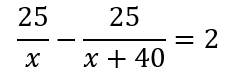
4. Умножим обе части уравнения на x (x+40) > 0.
25 (x+40) — 25x = 2x(x+40)
25x — 1000 — 25x = 2x2 + 80x
2x2 + 80x — 1000 = 0
x2 + 40x — 500 = 0
5. Найдём корни данного уравнения через дискриминант.
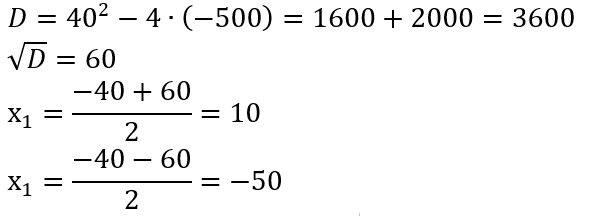
Скорость не может быть отрицательной, поэтому в ответ запишем 10 (км/ч).
Ответ: 10.
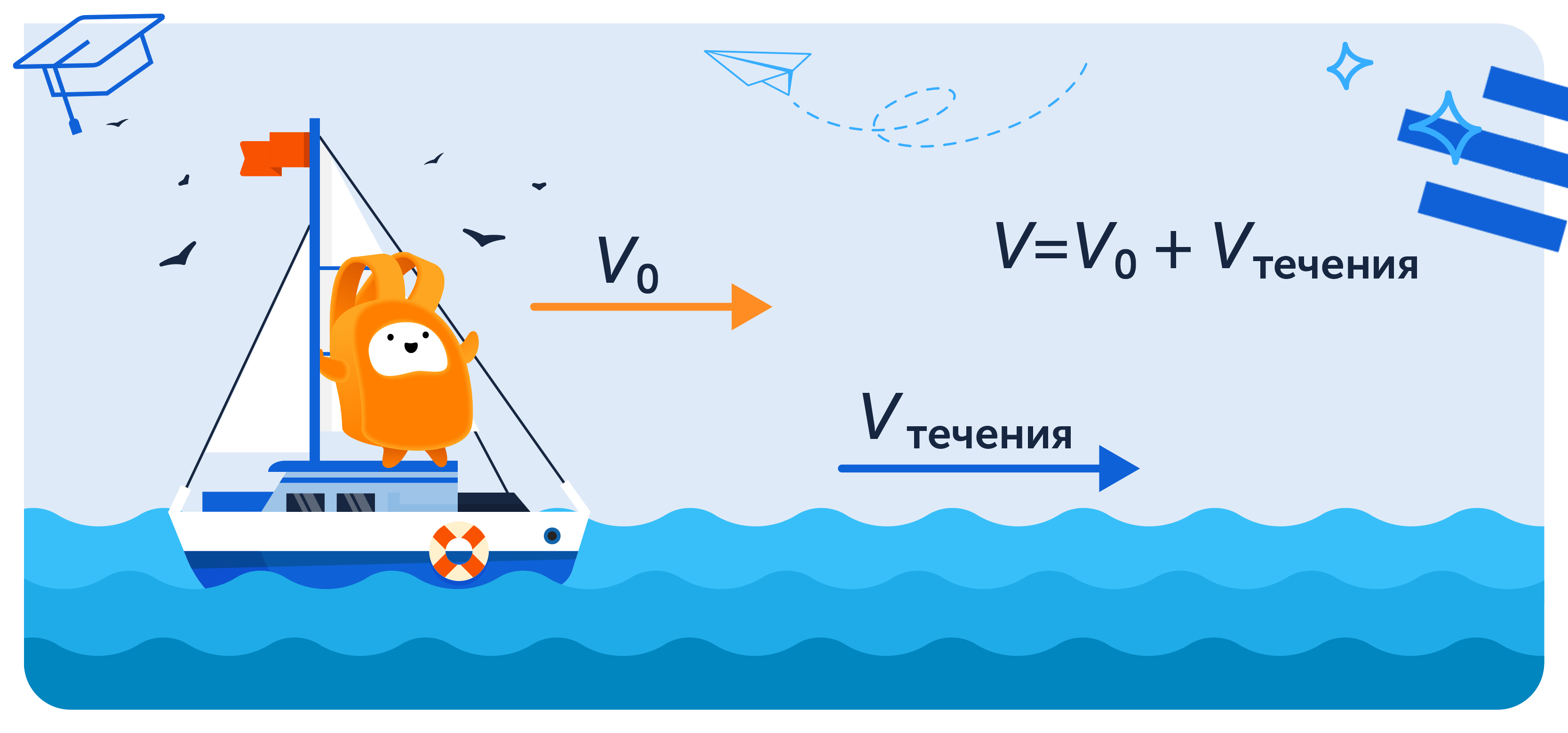
Решение текстовых задач на движение по воде
Задачи на движение по воде решаются по такому же алгоритму, что и задачи на движение по прямой, но с учётом скорости течения воды.
При движении по течению реки можно сказать, что течение «помогает» движению, поэтому к собственной скорости моторной лодки, катера, теплохода и других объектов будем прибавлять скорость течения.

При движении против течения реки можно сказать, что течение «мешает» движению, поэтому из собственной скорости объекта будем вычитать скорость течения.
Пример решения текстовой задачи из экзамена
Рассмотрим интересную задачу про яхту и плот. Обратим внимание, что:
-
плот мы признаем объектом, не имеющим собственной скорости, а значит, он движется со скоростью течения;
-
объект (яхта, моторная лодка, катер), движущийся в одном направлении с плотом, движется по течению.

Решение:
1. Составим таблицу. В задаче требуется узнать собственную скорость яхты, заменим её на неизвестную х. Получается, скорость яхты по течению равна х + 2 км/ч, а против течения — х – 2 км/ч.
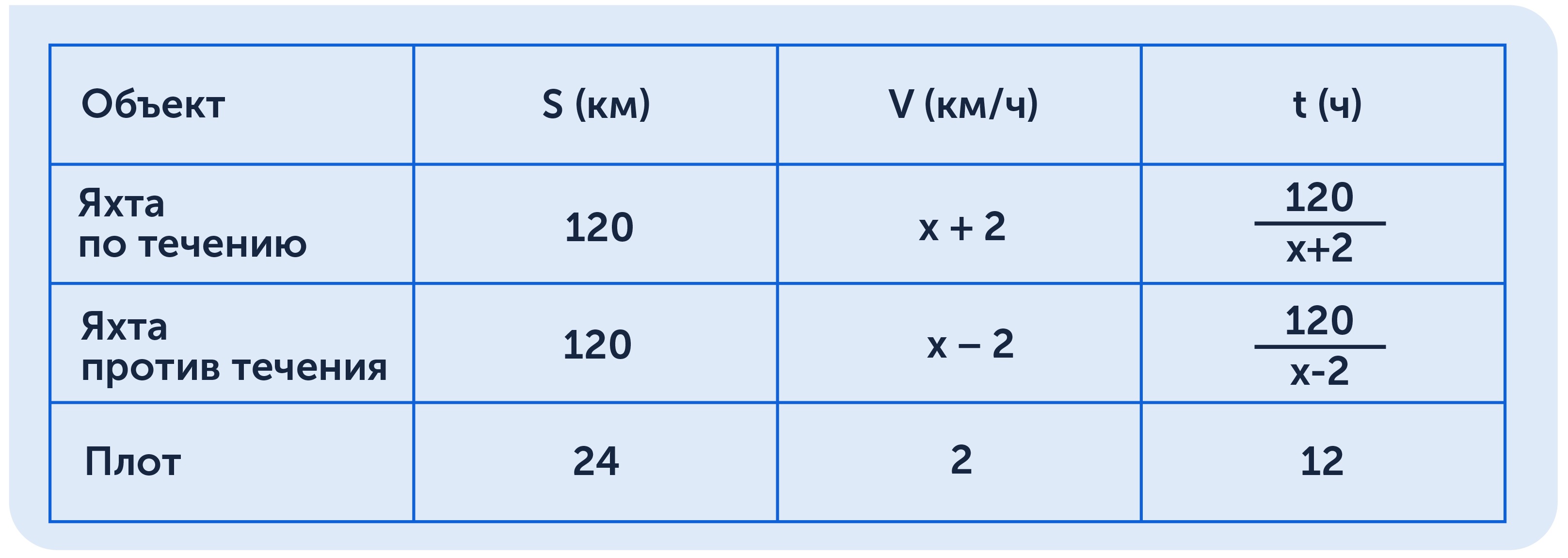
2. Учитываем, что плот прошёл 24 км со скоростью 2 км/ч (скорость течения), значит, он находился в движении 12 часов. Яхта вышла из пункта А через час после того, как отправился плот, следовательно, она была в движении 11 часов. Составим и решим уравнение.
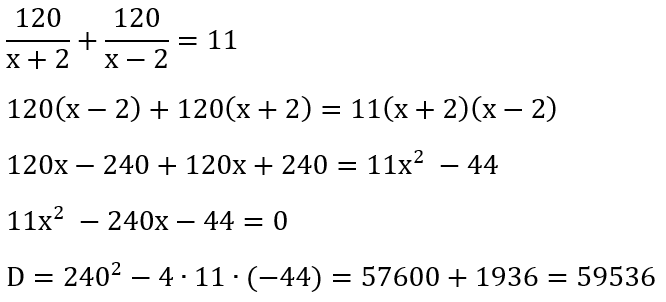
3. Подберём корень из дискриминанта. 59 536 больше 10 000, значит, корень из дискриминанта — трёхзначное число. 2402 = 57 600, 2502 = 62 500. Получается, искомое число лежит в диапазоне от 240 до 250, заканчивается либо на 4, либо на 6. Это 244 или 246. Проверим результат умножением. Подходит 244 × 244 = 59 536.
4. Остаётся посчитать корни уравнения.
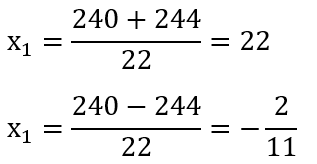
Скорость не может быть отрицательной, поэтому ответ задачи — 22 км/ч.
Ответ: 22.
Решение текстовых задач на работу
Работа в контексте текстовых задач — это выполнение какого-либо задания: изготовление деталей, наполнение бассейнов, укладка плитки, решение тестов. Принято обозначать выполненную работу латинской буквой А.
Производительность труда — работа, выполненная в единицу времени.
Чтобы найти производительность труда, необходимо объём выполненной работы (A) поделить на время (t), затраченное на выполнение этой работы. Производительность принято обозначать латинской буквой N.
Большинство экзаменационных задач на работу могут быть решены при помощи следующего алгоритма:
-
Составляем таблицу со столбцами: работа — A, производительность — N, время — t.
-
Обозначаем неизвестной х то, что требуется найти в задаче.
-
Заполняем два столбца таблицы в соответствии с введённой неизвестной и данными задачи.
-
Заполняем оставшийся «ключевой» столбец (чаще всего это столбец «Время») по формулам: A = N × t; N = A : t; t = A : N.
-
Составляем уравнение с данными ключевого столбца таблицы.
-
Решаем полученное уравнение и находим неизвестную.
-
Не забываем, что работа, время и производительность должны быть положительными.
Теперь разберём алгоритм решения на прототипе экзаменационного задания.
Пример решения текстовой задачи из экзамена

Решение:
1. Составим таблицу. Заменим производительность труда второго рабочего на х. Первый рабочий изготавливает в час на 8 деталей больше, значит, его производительность — x + 8.
Оба рабочих выполняют работу по изготовлению 209 деталей. Время выразим через формулу t = A × N. По условию задачи второму рабочему на выполнение заказа потребовалось на 8 часов больше. Производительность его работы ниже, значит, время работы больше. Тогда, если из времени работы второго рабочего мы вычтем время работы первого рабочего, получится 8 часов.

2. Составим и решим уравнение.
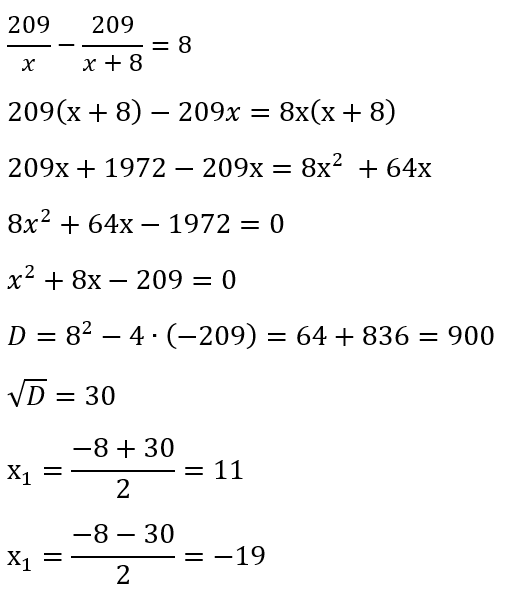
Производительность не может быть отрицательной, поэтому в ответ запишем 11.
Ответ: 11.
И ещё одна подсказка. Ответ любой текстовой задачи можно проверить, подставив полученное значение в таблицу. Если расхождения с условием нет, значит, вы всё сделали правильно.
А теперь предлагаем закрепить знания, ответив на вопросы теста на решение текстовых задач по математике.
Если всё это пока сложно для вас, не переживайте. И текстовые задачи, и любые сложные темы в ОГЭ и ЕГЭ по математике, а также по любым другим предметам поможем освоить на курсах подготовки к ОГЭ и ЕГЭ ИнтернетУрока.






















































 09 февраля 2024
09 февраля 2024  14 231
14 231
 Статья
Статья