Подготовка к олимпиаде по математике: советы и ресурсы

Подготовка к олимпиаде по математике требует серьёзного планирования, регулярных занятий, знания методик решения нестандартных задач. В этой статье рассказываем, как подготовиться к соревнованиям по математике, какие есть способы и как избежать типичных ошибок олимпиадников.

Какие бывают олимпиады?

Олимпиады по математике — настоящая битва умов, которая открывает перед школьником спектр возможностей: от развития логического мышления до поступления в престижные вузы на льготных условиях. 

Математические состязания различаются по уровню сложности, формату проведения и статусу:

• Всероссийская олимпиада школьников (ВсОШ) — самое массовое и престижное соревнование, которое включает четыре этапа: школьный, муниципальный, региональный и заключительный. Результаты победителей принимаются в каждом университете России.
• Перечневые олимпиады — соревнования из официального перечня Минобрнауки: дают льготы при поступлении в вуз, требуют личного присутствия.
• Проверочные олимпиады — соревнования для оценки уровня знаний и для получения опыта участия: проходят дистанционно, не дают льгот абитуриентам.

В 2025/26 учебном году победители и призёры ВсОШ и перечневых олимпиад получат право на зачисление в вуз без вступительных испытаний (БВИ) или 100 баллов за ЕГЭ по профильному предмету, согласно части 4 статьи 71 Федерального закона № 273-ФЗ «Об образовании в Российской Федерации». В числе прочего этими бонусами математические олимпиады привлекают школьников, которые планируют поступать на физмат в ведущие университеты страны. 

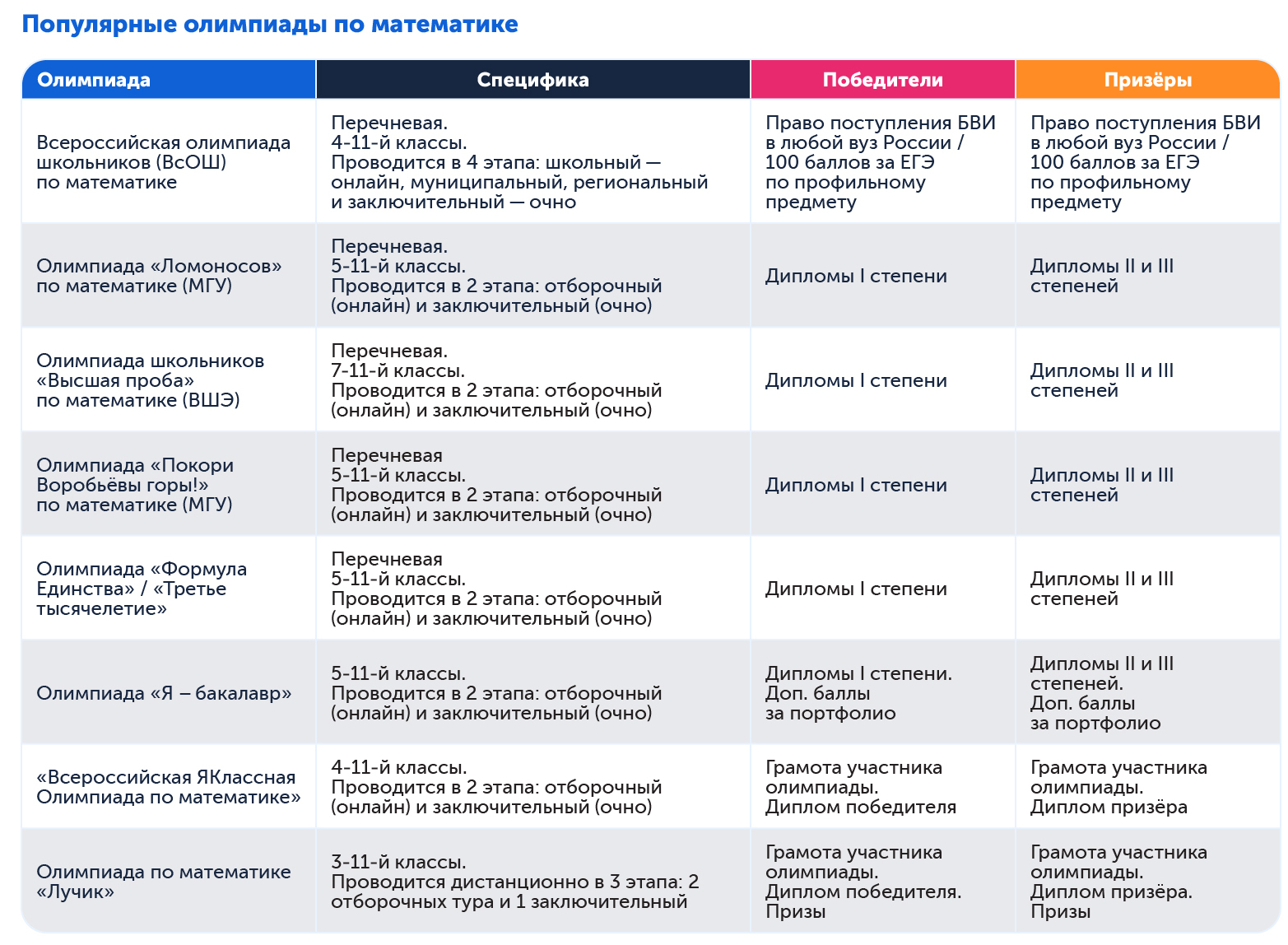
При выборе олимпиады следует ориентироваться на текущий уровень подготовки ученика и цели участия. Проверочные соревнования не дадут льгот при поступлении. Такие турниры — инструмент для определения пробелов в знании предмета.

Что особенного в олимпиадных задачах?

Олимпиадные задачи по математике сложнее школьных и тех, которые выпускники решают на ОГЭ и ЕГЭ. Для победы нужно проявить творческий подход, выйти за рамки привычных шаблонов. 

Чем отличаются олимпиадные задачи: 

• Повышенный уровень сложности. Олимпиадные задачи требуют гибкости ума, нестандартного подхода, крепкой математической базы, выходящей за рамки школьной программы.
• Нет единого стандарта. Будущим математикам предстоит самостоятельно подбирать уникальный алгоритм решения для каждого задания, в отличие от привычных школьных шаблонов.
• Разнообразие задач. От участников ждут знаний из самых разных областей математики: алгебры, геометрии, комбинаторики, теории чисел. Встречаются задачи на внимание, объёмно-пространственное мышление.

Есть и схожие с ГИА аспекты:

• Аргументация. Олимпиаднику важно уметь объяснить ответ и выбранную тактику решения — по тому же принципу, как в шести заданиях на ОГЭ и семи задачах на ЕГЭ по математике профильного уровня.  
• Ограниченное время. Необходимо показать результат в условиях жёсткого дедлайна.

Как подготовиться к олимпиаде по математике?

Подготовка к математическому состязанию состоит из трёх компонентов: работы с теорией, решения задач, оттачивания соревновательных скиллов. К призовым местам ведут структурированный подход и чёткое планирование.

Алгоритм, как подготовиться к олимпиаде по математике:

1. Определить цели участия, оценить уровень владения предметом. Для этого подойдут онлайн-турниры — например, онлайн-олимпиада «Лучик». Участие поможет выявить пробелы в знаниях и понять, сколько времени нужно на подготовку.
2. Выбрать 1–2 олимпиады по математике, в которых хотите участвовать. Рекомендуем изучить их регламент, критерии оценки, проанализировать свои сильные и слабые стороны.
3. Составить план подготовки. Распишите, в какие дни займётесь теорией, практикой, разбором ошибок. Укажите темы, которые необходимо разобрать подробнее.
4. Закрепить школьную программу. Это база. Без глубокого владения материалом не получится перейти к заданиям более сложного уровня.
5. Решать математические игры и головоломки — они помогают развить креативное мышление.
6. Сфокусироваться на интенсивной практике за 1–2 месяца до соревнования: решать прошлогодние варианты задач, участвовать в проверочных состязаниях.

В помощь будущим олимпиадникам ИнтернетУрок делится подборкой онлайн-ресурсов, которые помогут подготовиться к турнирам:

• ВсОШ — официальный сайт Всероссийской олимпиады школьников с заданиями прошлых лет;
• Турнир городов — официальный сайт «Турнира городов» с заданиями прошлых лет;
• Олимпиада.ру — крупнейший портал с информацией об олимпиадах, архивом задач прошлых лет и материалами для подготовки;
• Т-Образование — бесплатные образовательные программы для подготовки к олимпиадам;
• Яндекс Учебник — бесплатные курсы подготовки к школьным олимпиадам.

Помните, что переутомление не поможет победить. Важно заниматься регулярно, а не интенсивно. Сложность тестов рекомендуем повышать постепенно, внимательно анализировать ошибки и не забывать об отдыхе.

Кирилл Широбоков, учитель математики в петербургской частной школе «ИндиКид»:

«Учеников 5–7-х классов важно научить думать самостоятельно, а не “натаскать” на типовые задачи. 

Какие приёмы развивают самостоятельность:

1. Тренировать умение работать без подсказок. Даже дома можно создать условия, похожие на олимпиадную среду: посадить ребёнка одного на 40 минут с задачами и не помогать. Главное — не проверка, а последующий разбор: какие шаги ученик предпринимал, какой логикой шёл. Это формирует уверенность, учит анализировать свои действия.
2. Изменить условия задачи. Если ребёнок застрял, можно изменить параметры: увеличить или уменьшить числа, добавить новый элемент. Посмотрите, как изменится решение. Иногда в процессе ученик находит закономерность или упрощает задачу. Это то, что я называю “правилом большого пальца”: если стало проще — значит, ты на правильном пути. Такой способ развивает гибкость мышления, помогает видеть математику не как набор формул, а как живую систему взаимосвязей.
3. Работать с подвластными действиями. Полезно учить ребёнка пробовать простейшие операции с тем, что уже есть. Например, если в задаче про прямоугольник встречаются числа 6 и 4, можно перемножить их и увидеть: это не просто два числа, а стороны фигуры, их произведение даёт площадь. Так ученик понимает смысл формулы. Здесь важна роль наставника, нужно помочь понять, какие действия логичны, а какие — нет. 
4. Обучать пространственному анализу. Полезный навык даже на базовом уровне — следить за единицами измерения. На примерах дети интуитивно запоминают формулы, связи между величинами. Например, что скорость — это путь, делённый на время, ведь в единицах измерения километры стоят над часами, как в дроби.

Эти приёмы подходят в первую очередь детям 10–13 лет, у которых уже есть интерес к поиску, но ещё не хватает устойчивой логики. Сверхподготовки не требуется — всего лишь немного терпения, готовности обсуждать процесс, а не только результат. Главное, чтобы математика перестала быть “заданием с правильным ответом” и превратилась в увлекательную игру с мыслями».

Хорошо, когда родителям не нужно самостоятельно развивать у ребёнка базовый интерес к самостоятельному решению задач, а учебная программа школы пробуждает интерес к познанию. В онлайн-школе «ИнтернетУрок» занятие начинается с вовлекающего факта по теме уже пройденного материала или жизни вне школы. Ученик самостоятельно выбирает глубину изучения и уровень сложности ДЗ.

Каждый шаг урока — это выбор: пересмотреть ли видеоурок, посмотреть ли консультацию, потренироваться ли на тренажёрах или сразу перейти к ДЗ, какое ДЗ выполнить — тестовое или письменное. Ответов на задания нет в ГДЗ, школьники учатся думать сами. Как это выглядит на практике, приглашаем увидеть своими глазами. Дарим пробный доступ с полным функционалом на неделю. С ним вы наглядно увидите, какой формат обучения может развивать базовые навыки самостоятельного мышления. 

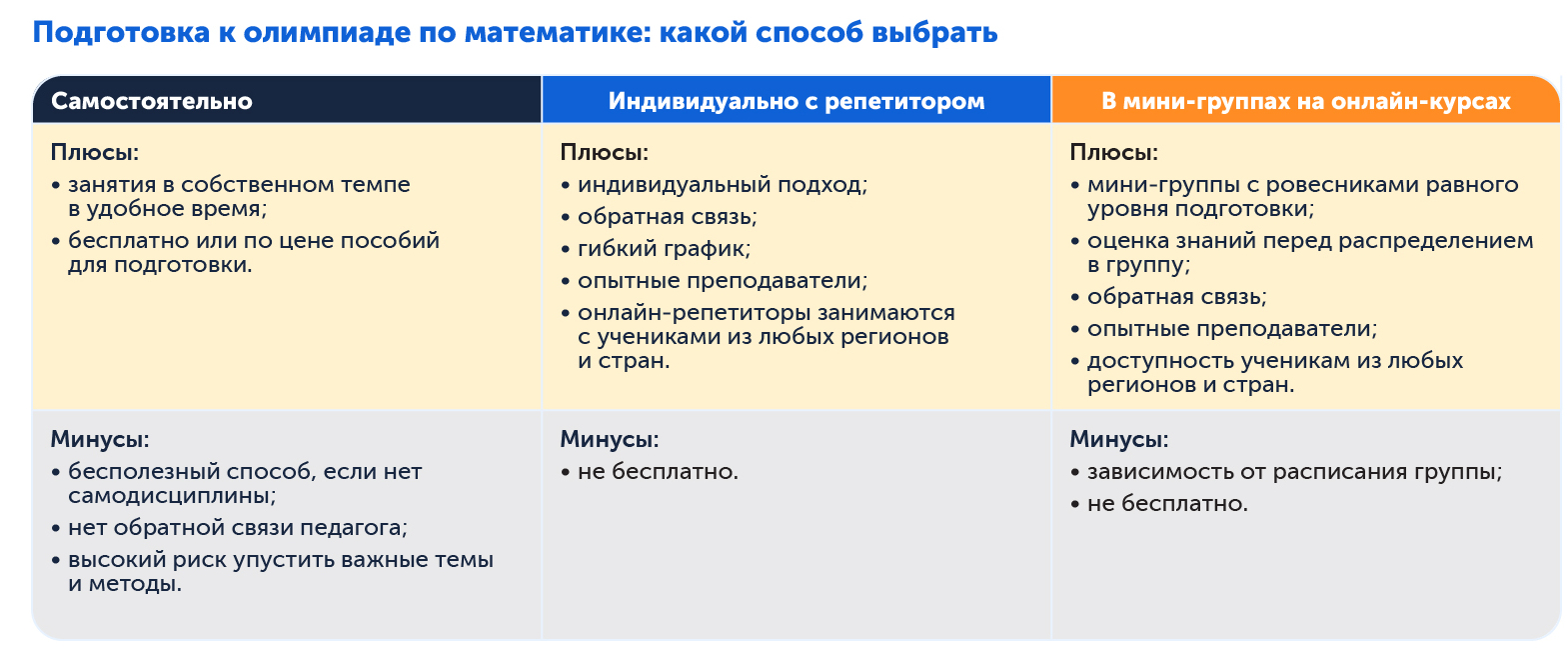
Как лучше готовиться: самостоятельно или с репетитором?

Выбор способа подготовки зависит от нескольких факторов: текущего уровня знаний, целей, времени до мероприятия и личных особенностей.

Самостоятельно

Самоподготовка подходит для целеустремлённых и дисциплинированных учеников. Выбравшим этот путь предстоит решать математические задачи разной сложности по вариантам заданий прошлых лет или из сборников задач. Школьных книг будет недостаточно, поэтому можно обратиться к вузовским учебникам и пособиям для олимпиадников.

Анна Жадан, методист онлайн-школы «ИнтернетУрок»:

«Полезно изучать и прорешивать олимпиадные задания прошлых лет. Структура задач и идеи решения часто повторяются. Решая эти задачи, вы тренируете технику, учитесь распознавать подводные камни, замечать, как формулируются условия, какие методы решения чаще используются, где прячутся хитрые допущения и как их превзойти. 

Также полезно работать с задачами из классических сборников олимпиадных задач, поскольку они предлагают системную подачу материала, позволяют увидеть эволюцию техник и методик, часто с примерами.

Важно не просто наращивать количество решённых задач, а качественно изучать темы со всех сторон:

1. освоить теорию, базовые принципы, примеры разной сложности; 
2. узнать хитрости и стандартные доказательные трюки; 
3. перейти к углублению знаний через нестандартные задачи, которые заставляют использовать те же инструменты иначе. 

Рекомендую выписывать критерии сходства между задачами:

• какие условия приводят к применению одного метода; 
• какие дают возможность комбинировать несколько подходов; 
• когда удобно перейти от исходной формулировки к знакомому шаблону решения; 
• как формулировка условий изменяет выбор техники. 

Такой всесторонний подход позволяет не застревать в узком наборе примеров, а развивает гибкость мышления, которая нужна на олимпиадах, где задача часто адаптирует известный метод под новую форму».

С репетитором 

Репетитор помогает подготовиться к олимпиаде, объясняет сложные темы, устраняет пробелы в знаниях. И главное: он расширяет кругозор по математике, выводит за рамки школьной программы и готовит ученика к конкретному состязанию. 

Важно, чтобы у репетитора был опыт подготовки именно к олимпиадной математике. Такой преподаватель воспитывает креативный подход к решению задач. Это редкий навык и экспертиза. Не в каждом городе есть такой педагог, поэтому разумно выбрать онлайн-репетитора. Так вы сможете заниматься с сильным педагогом из любой точки мира. 

В мини-группах с олимпиадниками

Если школьник нацелен на призовые места или победу, полезно заниматься в группе с учениками равного уровня, например на курсах углублённого физико-математического профиля для 8–11-х классов. В программе основные направления для подготовки к олимпиадам, а также программирование на Python, робототехника и другие темы, которые пригодятся выбравшим математику для ЕГЭ, учёбы, карьеры и жизни. Такие занятия подходят и тем, кто в нескольких шагах от призового места, и тем, кто только размышляет, стоит ли вообще участвовать в олимпиадах. Для каждого уровня подготовки свои группы.

Как избежать ошибок олимпиадника?

Начинающие участники часто совершают типичные ошибки, которые мешают становиться победителями состязаний. Делимся секретами, чего стоит избегать, чтобы достигнуть желаемых результатов.


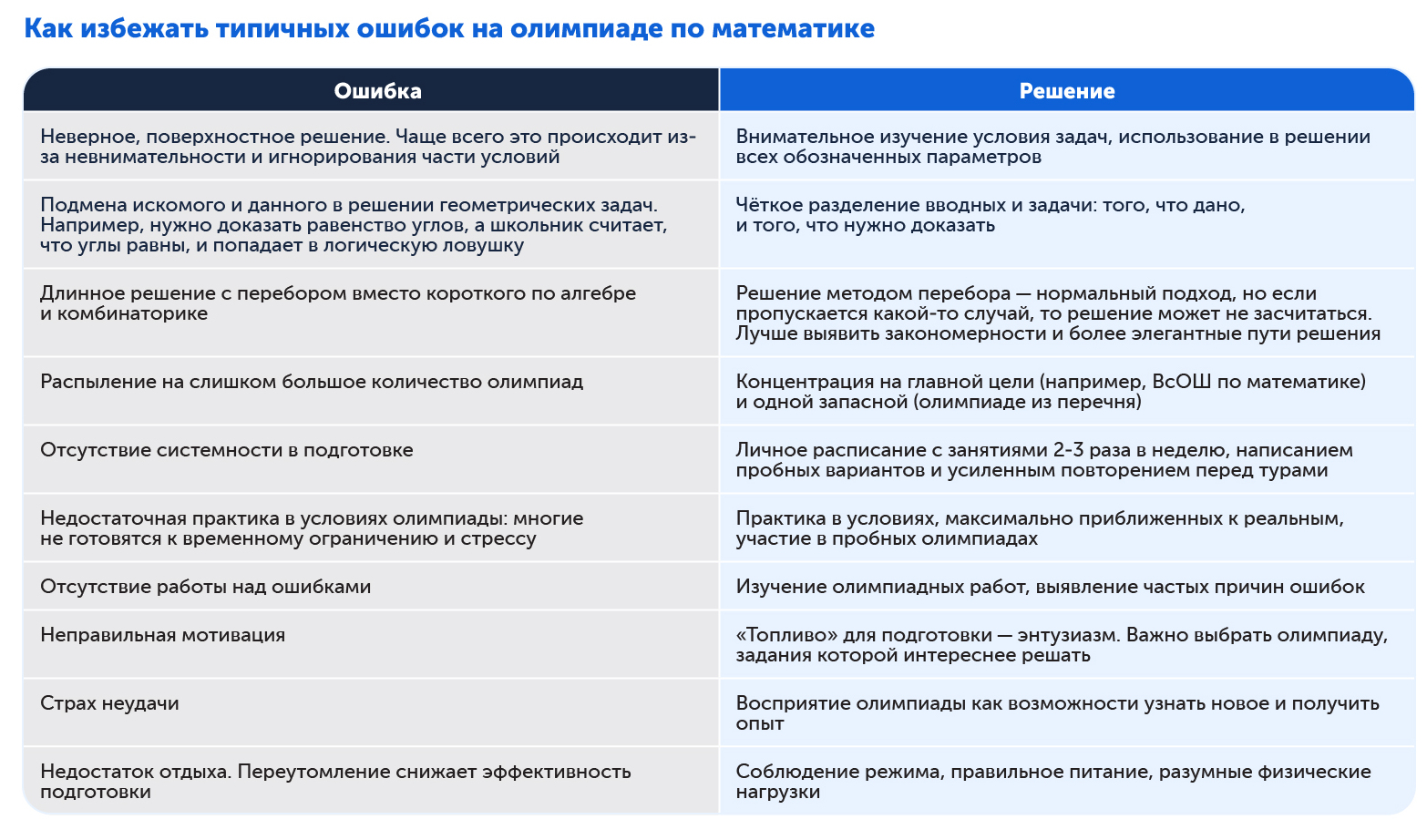
Избежать этих ошибок помогут грамотно выстроенный план подготовки и регулярная практика в решении олимпиадных задач.

По мнению редакции, оптимальная стратегия подготовки к олимпиаде такая: 

• самостоятельная практика на вариантах прошлых лет; 
• дополнительные занятия с опытным наставником по сложным темам и непонятным заданиям олимпиад; 
• занятия в мини-группах с олимпиадниками при опытной онлайн-школе. 

Такой подход даёт структурированные знания, восполняет пробелы в знаниях, развивает навык самостоятельного решения задач и готовит именно к заданиям олимпиадного типа.

Подготовка к олимпиаде по математике — долгосрочное вложение в образование и будущее. Систематические занятия, работа с опытными преподавателями, регулярная практика, правильный настрой помогают получить высокие баллы на олимпиадных заданиях. А подготовка в мини-группах позволяет найти ещё более креативные решения с олимпиадниками равного уровня.

Физико-математический профиль

Изучайте физику, математику и информатику
углублённо в 8-11 классах

Подробнее Оставить заявку

Учебные вопросы

Екатерина Хлуденёва, редакция журнала «ИнтернетУрок»

Домашняя школа «ИнтернетУрок» Б. Гнездниковский, 1 стр.2, Москва, 125375 8 (800) 775 4121